La ecuación
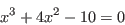 |
(2.1) |
tiene una raíz única en ![$[1, 2]$](img38.png) , observe la grafica de la función en la figura 2.7.
, observe la grafica de la función en la figura 2.7.
Figura 2.7:
Grafica del Ejemplo 4
|
|
Hay muchas formas para convertirla en la forma 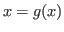 mediante un simple manejo algebraico.
Por ejemplo, si igualamos las funciones
mediante un simple manejo algebraico.
Por ejemplo, si igualamos las funciones
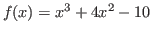 y
y 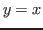 , para obtener las intersecciones que finalmente son los puntos fijos, que de manera equivalente es
, para obtener las intersecciones que finalmente son los puntos fijos, que de manera equivalente es
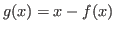 obtendríamos:
obtendríamos:
La cual se elige como 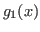 .
.
Por otro lado, si de la ecuación 2.1 se despeja la 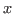 de segundo grado se tendría:
de segundo grado se tendría:
Esta expresión se elige como 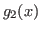 , cabe mencionar que nos da una solución positiva.
, cabe mencionar que nos da una solución positiva.
Finalmente para 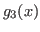 se elige de la forma
se elige de la forma
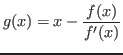 .
.
A continuación se muestran las expresiones obtenidas:
Dado que el intervalo de solución es ![$[1, 2]$](img38.png) , tomamos
, tomamos
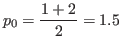 y aplicamos el algoritmo 2.
y aplicamos el algoritmo 2.
Tabla 2.1:
Iteraciones del Punto Fijo para Ejemplo 4.
| [gray]0.9i |
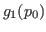 |
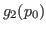 |
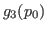 |
|
| 1 |
-0.8750000000 |
-0.8750000000 |
-0.8750000000 |
|
| 2 |
6.7324218750 |
2.5304360390 |
1.2389878035 |
|
| 3 |
-469.7200317383 |
0.7750910521 |
1.3647334576 |
|
| 4 |
102754568.0 |
1.6687980890 |
1.3652287722 |
|
| 5 |
-1084934371998527551176704 |
1.2102226019 |
1.3652306795 |
|
| 6 |
inf |
1.4446905851 |
|
|
| 7 |
NaN |
1.3245767355 |
|
|
| 8 |
NaN |
1.3860507011 |
|
|
| 9 |
NaN |
1.3545730114 |
|
|
| 10 |
NaN |
1.3706853390 |
|
|
| 11 |
NaN |
1.3624360561 |
|
|
| 12 |
NaN |
1.3666603565 |
|
|
| 13 |
NaN |
1.3644964695 |
|
|
| 14 |
NaN |
1.3656061888 |
|
|
| 15 |
NaN |
1.3650385141 |
|
|
| 16 |
NaN |
1.3653270006 |
|
|
| 17 |
NaN |
1.3651808500 |
|
|
| 18 |
NaN |
1.3652548790 |
|
|
| 19 |
NaN |
1.3652179241 |
|
|
| 20 |
NaN |
1.3652364016 |
|
|
| 21 |
NaN |
1.3652271032 |
|
|
| 22 |
NaN |
1.3652306795 |
|
|
|
La tabla 2.1 muestra las iteraciones del algoritmo del Punto Fijo para el ejemplo 4. Observando los resultados obtenidos concluimos lo siguiente:
- La función
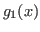 diverge luego de 5 iteraciones.
diverge luego de 5 iteraciones.
- La función
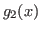 converge a la raíz luego de 22 iteraciones.
converge a la raíz luego de 22 iteraciones.
- La función
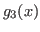 converge a la raíz luego de 5 iteraciones.
converge a la raíz luego de 5 iteraciones.
- Aunque
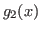 y
y 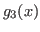 convergen a la raíz,
convergen a la raíz, 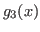 necesita un número considerablemente menor de iteraciones.
necesita un número considerablemente menor de iteraciones.
Finalmente la raíz es
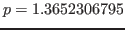 .
.
Demuestre que
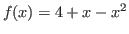 tiene una raíz en el intervalo
tiene una raíz en el intervalo ![$[0, 20]$](img35.png) y utlice el método de punto fijo para determinar una aproximación a la raíz que sea precisa al
menos hasta
y utlice el método de punto fijo para determinar una aproximación a la raíz que sea precisa al
menos hasta 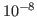 .
.
La grafica de
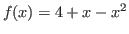 se puede ver en la figura 2.8.
se puede ver en la figura 2.8.
Figura 2.8:
Grafica del Ejemplo 5
|
|
Se puede ver que la gráfica tiene dos raíces y efectivamente una de ellas se encuentra en el intervalo dado ![$[0, 20]$](img35.png) . Resolviendo la ecuación por la formula
general se obtiene:
. Resolviendo la ecuación por la formula
general se obtiene:
Obviamente en este punto la raíz ha sido encontrada y no hay necesidad de aplicar el método del Punto Fijo, utilizamos un ejemplo sencillo y comprobable para que el
método sea claro y con resultado comprobable, para posteriormente resolver raíces que no son posibles de obtener analíticamente.
El punto de partida para todos los casos es:
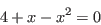 |
(2.2) |
Para  igualamos las funciones
igualamos las funciones
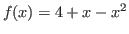 y
y  , para obtener las intersecciones que son los puntos fijos, obtendríamos:
, para obtener las intersecciones que son los puntos fijos, obtendríamos:
La cual se elige como 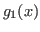 .
.
Por otro lado, si se despeja la 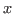 de segundo grado de la expresión 2.2 se tendría:
de segundo grado de la expresión 2.2 se tendría:
Esta expresión se elige como 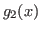 .
.
Finalmente para 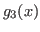 se elige de la forma
se elige de la forma
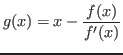 .
.
A continuación se muestran las expresiones obtenidas:
Dado que el intervalo de solución es ![$[1, 2]$](img38.png) , tomamos
, tomamos
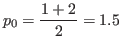 y aplicamos el algoritmo 2 obteniendo los siguientes resultados:
y aplicamos el algoritmo 2 obteniendo los siguientes resultados:
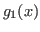 diverge.
diverge.
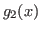 converge luego de 13 iteraciones.
converge luego de 13 iteraciones.
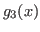 converge luego de 7 iteraciones.
converge luego de 7 iteraciones.
La raíz encontrada por el método es
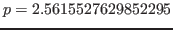 .
.
![]() . Ésta técnica recibe el nombre de iteración de punto fijo o iteración funcional. Este procedimiento se describe detalladamente en el
algoritmo 2 y se muestra en la figura 2.6.
. Ésta técnica recibe el nombre de iteración de punto fijo o iteración funcional. Este procedimiento se describe detalladamente en el
algoritmo 2 y se muestra en la figura 2.6.
![]() mediante un simple manejo algebraico.
Por ejemplo, si igualamos las funciones
mediante un simple manejo algebraico.
Por ejemplo, si igualamos las funciones
![]() y
y ![]() , para obtener las intersecciones que finalmente son los puntos fijos, que de manera equivalente es
, para obtener las intersecciones que finalmente son los puntos fijos, que de manera equivalente es
![]() obtendríamos:
obtendríamos:
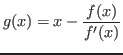 .
.
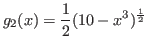
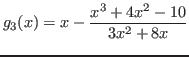
![]() , tomamos
, tomamos
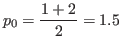 y aplicamos el algoritmo 2.
y aplicamos el algoritmo 2.
![]() .
.
![]() se puede ver en la figura 2.8.
se puede ver en la figura 2.8.
![]() . Resolviendo la ecuación por la formula
general se obtiene:
. Resolviendo la ecuación por la formula
general se obtiene:
![]() igualamos las funciones
igualamos las funciones
![]() y
y ![]() , para obtener las intersecciones que son los puntos fijos, obtendríamos:
, para obtener las intersecciones que son los puntos fijos, obtendríamos:
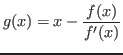 .
.
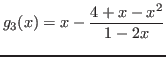
![]() , tomamos
, tomamos
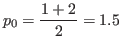 y aplicamos el algoritmo 2 obteniendo los siguientes resultados:
y aplicamos el algoritmo 2 obteniendo los siguientes resultados:
![]() .
.
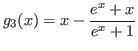
![]() y obtenemos los siguientes resultados:
y obtenemos los siguientes resultados:
![]() .
.